


Next: Projective Invariants & the
Up: Linear Algebra and Homogeneous
Previous: Lines in the Plane
A point A is fixed by a collineation with matrix H exactly when 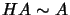 ,
i.e.
,
i.e.
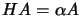 for some scalar
for some scalar 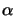 .
In other
words, A must be a right eigenvector of H. Since an
.
In other
words, A must be a right eigenvector of H. Since an
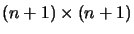 matrix typically has n+1 distinct eigenvalues, a
collineation in
matrix typically has n+1 distinct eigenvalues, a
collineation in
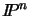 typically has n+1 fixed points, although
some of these may be complex.
typically has n+1 fixed points, although
some of these may be complex.
H maps the line through any two fixed points A and B onto
itself:
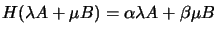 .
In
addition, if A and B have the same eigenvalue (
.
In
addition, if A and B have the same eigenvalue (
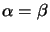 ),
),
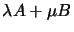 is also an eigenvector and the entire line AB is
pointwise invariant. In fact, the pointwise fixed subspaces of
is also an eigenvector and the entire line AB is
pointwise invariant. In fact, the pointwise fixed subspaces of 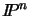 under H correspond exactly to the eigenspaces of H's repeated
eigenvalues (if any).
under H correspond exactly to the eigenspaces of H's repeated
eigenvalues (if any).
Exercise 2.5
:
Show that the matrix associated with a plane translation has a triple
eigenvalue, but that the corresponding eigenspace is only two
dimensional. Provide a geometric interpretation of this.
Exercise 2.6
:
In 3D Euclidean space, consider a rotation by angle
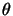
about the
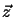
axis. Find the eigenvalues and eigenspaces, prove
algebraically that the rotation axis is pointwise invariant, and show
that in addition the ``circular points'' with complex coordinates
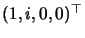
and
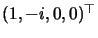
are fixed.



Next: Projective Invariants & the
Up: Linear Algebra and Homogeneous
Previous: Lines in the Plane
Bill Triggs
1998-11-13
![]() ,
i.e.
,
i.e.
![]() for some scalar
for some scalar ![]() .
In other
words, A must be a right eigenvector of H. Since an
.
In other
words, A must be a right eigenvector of H. Since an
![]() matrix typically has n+1 distinct eigenvalues, a
collineation in
matrix typically has n+1 distinct eigenvalues, a
collineation in
![]() typically has n+1 fixed points, although
some of these may be complex.
typically has n+1 fixed points, although
some of these may be complex.
![]() .
In
addition, if A and B have the same eigenvalue (
.
In
addition, if A and B have the same eigenvalue (
![]() ),
),
![]() is also an eigenvector and the entire line AB is
pointwise invariant. In fact, the pointwise fixed subspaces of
is also an eigenvector and the entire line AB is
pointwise invariant. In fact, the pointwise fixed subspaces of ![]() under H correspond exactly to the eigenspaces of H's repeated
eigenvalues (if any).
under H correspond exactly to the eigenspaces of H's repeated
eigenvalues (if any).