Camera calibration:

Assuming that the camera performs a exact perspective projection (see 1.1.2), we have seen that the image formation process can be expressed as a projective mapping from $I\!\!P^{3}$ to $I\!\!P^{2}$. Projective camera calibration is the computation of the projection matrix associated with this mapping. This is usually done using a set of points whose 3D locations $(X, Y, Z, T)^{\top}$are known. If a pint projects to pixel coordinates (u,v), the projection equations can be written:

$$\left( \begin{array}{c} \lambda u\\ \lambda v\\ \lambda \end{... ... = P \left( \begin{array}{c} X\\ Y\\ Z\\ 1 \end{array}\right)$$

Taking ratios to eliminate the unknown scale factor $\lambda$, we have:

 

$$\frac {p_{11}x + p_{12}y + p_{13}z + p_{14}} {p_{31}x + p_{32}y + p_{33}z + p_{34}}$$ u =

$$\frac {p_{21}x + p_{22}y + p_{23}z + p_{24}} {p_{31}x + p_{32}y + p_{33}z + p_{34}}$$ v = (2.1)

As P is only defined up to an overall scale factor, this system has 11 unknowns. At least 6 points are required for a unique solution, but usually many more points are used in a least squares optimization that minimizes the effects of measurement uncertainty.

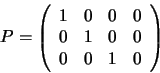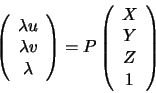
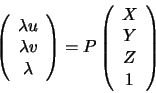
The projection matrix P contains both interior and exterior camera parameters. We will not consider the decomposition process here, as the exterior orientation/interior calibration distinction is only meaningful when projective space is reduced to Euclidean.

Exercise 2.2   : Assuming perspective projection centered at the origin onto plane z=1, and a $\vec{x}, \vec{y}$ image reference frame corresponding to the $\vec{x}, \vec{y}$ directions of the 3D reference frame, prove that the projection matrix P has the form

$$P = \left( \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{array}\right)$$

The null space of P (the set of X such that PX=0) corresponds to which 3D point X? What does the 3D point (x, y, 0) project to?