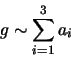A projective basis for
![]() is any set of n+2 points of
is any set of n+2 points of
![]() ,
no n+1 of which lie in a hyperplane. Equivalently, the
,
no n+1 of which lie in a hyperplane. Equivalently, the
![]() matrix formed by the column vectors of any n+1 of
the points must have full rank.
matrix formed by the column vectors of any n+1 of
the points must have full rank.
It is easily checked that
![]() forms a basis, called the canonical basis. It contains the
points at infinity along each of the n coordinate axes, the origin,
and the unit point
forms a basis, called the canonical basis. It contains the
points at infinity along each of the n coordinate axes, the origin,
and the unit point
![]() .
Any basis can be
mapped into this standard form by a suitable collineation.
.
Any basis can be
mapped into this standard form by a suitable collineation.
Property: A collineation on
A full proof can be found in [23]. We will just check
that there are the right number of constraints to uniquely characterize the
collineation. This is described by an
![]() matrix
A, defined up to an overall scale factor, so it has
(n + 1)2-1=
n(n+2) degrees of freedom. Each of the n+2 basis point images
matrix
A, defined up to an overall scale factor, so it has
(n + 1)2-1=
n(n+2) degrees of freedom. Each of the n+2 basis point images
![]() provides n constraints (n+1 linear equations
defined up a common scale factor), so the required total of n(n+2)constraints is met.
provides n constraints (n+1 linear equations
defined up a common scale factor), so the required total of n(n+2)constraints is met.