


Next: Desargues Theorem
Up: Hyperplanes and Duality
Previous: Hyperplanes and Duality
The set of all points in
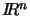 whose coordinates satisfy a
linear equation
whose coordinates satisfy a
linear equation
is called a hyperplane. Substituting homogeneous coordinates
Xi = xi/xn + 1 and multiplying out, we get a
homogeneous linear equation that represents a hyperplane in
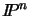 :
:
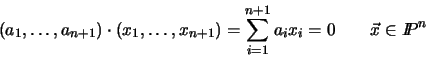 |
(2.2) |
Notice the symmetry of equation (2.2) between the
hyperplane coefficients
(a1, ..., an + 1) and the point
coefficients
(x1, ..., xn + 1). For fixed 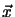 and variable
and variable
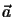 ,
(2.2) can also be viewed as the equation
characterizing the hyperplanes
,
(2.2) can also be viewed as the equation
characterizing the hyperplanes 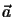 passing through a given point
passing through a given point
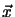 .
In fact, the hyperplane coefficients
.
In fact, the hyperplane coefficients 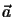 are also only
defined up to an overall scale factor, so the space of all hyperplanes
can be considered to be another projective space called the dual
of the original space
are also only
defined up to an overall scale factor, so the space of all hyperplanes
can be considered to be another projective space called the dual
of the original space
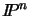 .
By the symmetry of (2.2),
the dual of the dual is the original space.
.
By the symmetry of (2.2),
the dual of the dual is the original space.
An extremely important duality principle follows from this symmetry:
Duality Principle: For any projective result established using points and hyperplanes,
a symmetrical result holds in which the roles of hyperplanes and points
are interchanged: points become planes, the points in a plane become the
planes through a point, etc.
For example, in the projective plane, any two distinct points define a
line (i.e. a hyperplane in 2D). Dually, any two distinct lines
define a point (their intersection). Note that duality only holds
universally in projective spaces: for example in the affine plane
parallel lines do not intersect at all.



Next: Desargues Theorem
Up: Hyperplanes and Duality
Previous: Hyperplanes and Duality
Bill Triggs
1998-11-13
![]() whose coordinates satisfy a
linear equation
whose coordinates satisfy a
linear equation