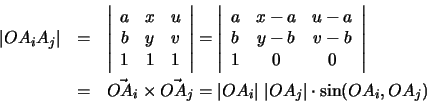Cross Ratios of Pencils of Lines

Let U and V be two lines in the projective plane, defined by their dual coordinate vectors. Consider a set of lines $\{W_{i}\}$defined by:

$$W_{i} = \lambda_{i} U + \mu_{i} V$$

with the $(\lambda_{i}, \mu_{i})$ defined up to scale as usual. $\{W_{i}\}$ belongs to the pencil of lines through the intersection of U and V (c.f. section 2.2.1), so each W_i passes through this point. As in section 3.1.1, the cross ratio $\{W_{1}, W_{2} ; W_{3}, W_{4}\}$is defined to be the cross ratio of the four homogeneous coordinate pairs $(\lambda_{i}, \mu_{i})$. Dually to points, we have:

Theorem: The cross ratio of any four lines of a pencil is invariant under collineations.

Cross ratios of collinear points and coincident lines are linked as follows:

Theorem: The cross ratio of four lines of a pencil equals the cross ratio of their points of intersection with an arbitrary fifth line transversal to the pencil (i.e. not through the pencil's centre) -- see fig. 3.1.

  

Figure 3.1: The cross ratio of four lines of a pencil

In fact, we already know that the cross ratios of the intersection points must be the same for any two transversal lines, since the lines correspond bijectively to one another under a central projection, which is a collineation.

The simplest way to establish the result is to recall the line intersection formulae of section 2.2.1. If U and Vare the basis 3-vectors for the line pencil, and L is the transversal line, the intersection points of L with U, V and $\lambda U + \mu V$ are respectively $L\times U$, $L\times V$ and $\lambda (L\times U)+\mu (L\times V)$. In other words, the $(\lambda, \mu)$coordinates of a line in the basis $\{U,V\}$ are the same as the $(\lambda, \mu)$ coordinates of its intersection with L in the basis $\{L\times U,L\times V\}$. Hence, the two cross ratios are the same.

To establish the result, we will consider a particular transversal line: the line at infinity. Let ax₀ + bx₁ + cx₂ = 0 be the equation defining U and dx₀ + ex₁ + fx₂ = 0 the one corresponding to V. Therefore the one associated to $\lambda U + \mu V$ is:

$$(\lambda a + \mu d)x_{0} + (\lambda b + \mu e) x_{1} + (\lambda c + \mu f) x_{2} = 0$$

This line intersect the line at infinity at a point with coordinates:

$$( - (\lambda b + \mu e), (\lambda a + \mu d), 0)$$

If we consider two reference points M and N being the intersection with line U and V, i.e. the points with coordinates

$$(-b, a, 0)^{t}, \qquad (-e, d, 0)^{t}$$

the generic point can therefore be described as $\lambda M + \mu N$. Therefore the intersection of line W_i with the line at infinity has the coordinates $(\lambda_{i}, \mu_{i})$ on the line [M, N], and therefore from the definition their cross ratios coincide. $\sqcup \!\!\!\! \sqcap$

Another way to prove the result is to show that cross ratios of lengths along the transversal line can be replaced by cross ratios of angle sines, and hence are independent of the transversal line chosen (c.f fig. 3.1):

$$\frac{\overline{AC}\cdot\overline{BC}} {\overline{AD}\cdot... ...}} = \frac{\sin(OA,OC)\;\sin(OB,OD)}{\sin(OA,OD)\;\sin(OB,OC)}$$ (3.3)

However, this is quite a painful way to compute a cross ratio. A more elegant method uses determinants:

Theorem (Möbius): Let $L_{i}, i=1,\ldots, 4$ be any four lines intersecting in O, and $A_i, i=1,\ldots, 4$ be any four points respectively on these lines, then

$$\{L_{1},L_{2} ; L_{3},L_{4}\} = \frac{\mid OA_{1}A_{3}\mid\;... ..._{2}A_{4}\mid} {\mid OA_{1}A_{4}\mid\;\;\mid OA_{2}A_{3}\mid}$$ (3.4)

where $\mid OA_{i}A_{j}\mid$ denotes the determinant of the $3\times3$matrix whose columns are the homogeneous coordinate vectors of points O, A_i and A_j.

This 19th century result extends gracefully to higher dimensions. To prove it, let (a,b, 1), (x,y, 1) and (u,v, 1) be the normalized affine coordinate vectors of O, A_i and A_j. Then

$$\begin{eqnarray*}\left\vert O A_i A_j\right\vert &=& \left\vert \begin{array}{cc... ...c{OA_{j}} = \vert OA_i\vert\;\vert OA_j\vert\cdot\sin(OA_i,OA_j) \end{eqnarray*}$$

The vector's lengths cancel out of the cross ratio of these terms, and if the coordinate vectors do not have affine normalization, the scale differences cancel out too. $\sqcup \!\!\!\! \sqcap$