


Next: Recognition with Invariants
Up: Harmonic Ratios and Involutions
Previous: The Complete Quadrangle
Definition: An involution is non-trivial projective collineation H whose square
is the identity:
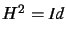 .
.
Property: The mapping taking a point to its harmonic conjugate is an involution.
By the definition of a harmonic pair, the mapping is its own inverse.
Using the cross ratio formula (3.2), it is straightforward
to check that it is also projective.

Exercise 3.7
:
Consider the affine line,
i.e. the projective line with the point
at infinity fixed. Show that the only affine involutions (projective
involutions fixing the point at infinity) are reflections about a fixed
point (
e.g. 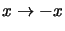
,
reflection about 0). Deduce that on the
projective line, all involutions with one fixed point have two fixed
points, and thence that they map points to their harmonic conjugates
with respect to these two fixed points.
Exercise 3.8
:
(NB: This is an algebraic continuation of the previous exercise). Let
a collineation
H be represented by a
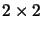
matrix as in
exercise
3.1. Prove that if
H is an involution then
a=-
d. Show that
H always has two distinct fixed points, either
both real or both complex. Give an
H that fixes the complex points
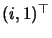
and
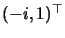
,
and show that if
x'=
Hx, then
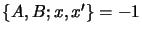
.
Given the invariance of the cross ratio under
complex collineations, show that all involutions of the projective
line map points to their harmonic conjugates with respect to the two
fixed points of the involution.
Involutions are useful when dealing with images of symmetrical objects.
Consider the simple case of a planar object with reflection symmetry, as in
fig. 3.5.
Figure 3.5:
Perspective view of a planar symmetrical shape
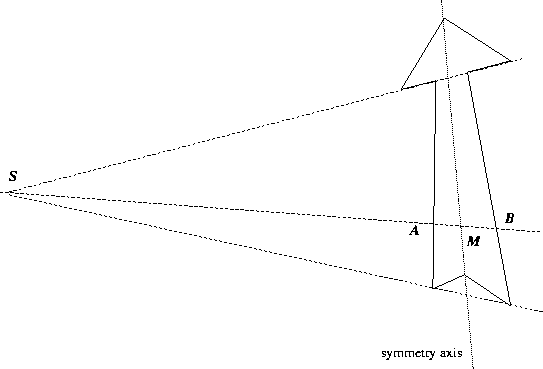 |
In 3D, the lines joining corresponding points of the object are
parallel. In the image, all such lines meet at the projection of the
associated point at infinity S. The projection of the line of symmetry
consists of points conjugate to S with respect of pairs of
corresponding points on the shape. There is a plane involution of the
image mapping points on the object to their opposites, and fixing Sand each point of the symmetry axis. Also, any line through any two
points of the figure meets the line through the two opposite points on
the axis: hence the axis is easy to find given a few
correspondences. All this extends to 3D symmetries: see
[22] chapter 8.



Next: Recognition with Invariants
Up: Harmonic Ratios and Involutions
Previous: The Complete Quadrangle
Bill Triggs
1998-11-13
![]()