


Next: Summary
Up: A Hierarchy of Geometries
Previous: Defining an Affine Restriction
From Affine to Euclidean Space
Here, by Euclidean space we actually mean space under the group of
similarity transforms, i.e. we allow uniform changes of scale in
addition to rigid displacements. This permits a very elegant algebraic
formulation, and in any case scale can never be recovered from images,
it can only be derived from prior knowledge or calibration. (You can
never tell from images whether you are looking at the real world or a
reduced model). In practice, Euclidean information is highly
desirable as it allows us to measure angles and length ratios.
Last century, Laguerre showed that Euclidean structure is given by the
location in the plane at infinity
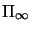 of a distinguished
conic, whose equation in a Euclidean coordinate system is
of a distinguished
conic, whose equation in a Euclidean coordinate system is
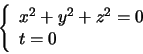 |
(4.1) |
This is known as the absolute conic 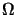 [13,23]. All points lying on it have complex
coordinates so it is a little difficult to picture, but for the most
part it behaves just like any other conic.
[13,23]. All points lying on it have complex
coordinates so it is a little difficult to picture, but for the most
part it behaves just like any other conic.
Exercise 4.3
:
Show that the absolute conic
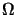
is mapped onto itself under
scaled Euclidean transformations. From there, show that the
corresponding image conic is invariant under rigid displacements of
the camera, provided that the camera's internal parameters remain
unchanged.
As in the projective to affine case, prior Euclidean information is
needed to recover Euclidean structure from affine space. Perhaps the
easiest way to do this is to reconstruct known circles in 3D space.
Algebraically, each such circle intersects
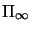 in exactly
two complex points, and these always belong to
in exactly
two complex points, and these always belong to 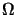 [23].
[23]. 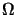 itself can be reconstructed from three
such circles. Let the resulting equation be
itself can be reconstructed from three
such circles. Let the resulting equation be
A change of coordinates is needed to bring 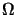 into the form
of equation (4.1). As the matrix Q is symmetric, there
is an orthogonal matrix P such that:
into the form
of equation (4.1). As the matrix Q is symmetric, there
is an orthogonal matrix P such that:
Setting X'=PX, we have:
With a further rescaling along each axis, we get equation
(4.1).
Another way to proceed is to use the basic extended Euclidean
invariant: the angle 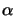 between two coplanar lines L and L'.
Such angles also put a constraint on
between two coplanar lines L and L'.
Such angles also put a constraint on 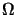 and can be used to
compute it. Let A and A' be the intersections of the two lines
with
and can be used to
compute it. Let A and A' be the intersections of the two lines
with
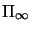 .
Let I and J be the intersections with
.
Let I and J be the intersections with
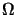 of the (line at infinity in the) plane defined by these two
lines. Laguerre's formula states that:
of the (line at infinity in the) plane defined by these two
lines. Laguerre's formula states that:
We can write I=A+tA',
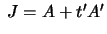 .
With this notation,
.
With this notation,
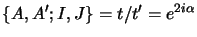 .
If we require that both I and J lie
on
.
If we require that both I and J lie
on 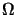 we get the constraint equations
we get the constraint equations
| t2 A'TQA' + 2 t ATQA' + ATQA |
= |
0 |
|
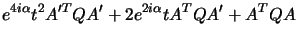 |
= |
0 |
(4.2) |
A polynomial constraint on Q is easily derived.
Eliminate t2 between the above equations:
extract t from this
and substitute into (4.2) to provide a quadratic polynomial
constraint on Q:
Theoretically, the absolute conic 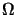 can be computed from the
above constraint given 5 known angles. However, in practice there does
not seem to be a closed form solution and in our experiments we have
used different Euclidean constraints. But the above discussion does
clearly show the relationships between the different layers of
projective, affine and Euclidean reconstruction, and specifies exactly
what structure needs to be obtained in each case.
can be computed from the
above constraint given 5 known angles. However, in practice there does
not seem to be a closed form solution and in our experiments we have
used different Euclidean constraints. But the above discussion does
clearly show the relationships between the different layers of
projective, affine and Euclidean reconstruction, and specifies exactly
what structure needs to be obtained in each case.



Next: Summary
Up: A Hierarchy of Geometries
Previous: Defining an Affine Restriction
Bill Triggs
1998-11-13
![]() of a distinguished
conic, whose equation in a Euclidean coordinate system is
of a distinguished
conic, whose equation in a Euclidean coordinate system is
![]() in exactly
two complex points, and these always belong to
in exactly
two complex points, and these always belong to ![]() [23].
[23]. ![]() itself can be reconstructed from three
such circles. Let the resulting equation be
itself can be reconstructed from three
such circles. Let the resulting equation be
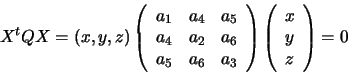
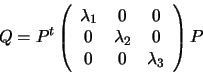
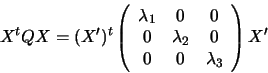
![]() between two coplanar lines L and L'.
Such angles also put a constraint on
between two coplanar lines L and L'.
Such angles also put a constraint on ![]() and can be used to
compute it. Let A and A' be the intersections of the two lines
with
and can be used to
compute it. Let A and A' be the intersections of the two lines
with
![]() .
Let I and J be the intersections with
.
Let I and J be the intersections with
![]() of the (line at infinity in the) plane defined by these two
lines. Laguerre's formula states that:
of the (line at infinity in the) plane defined by these two
lines. Laguerre's formula states that: