Derivation of Kruppa's Equations

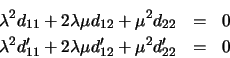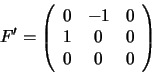
Let F be the fundamental matrix of the stereo rig. Change image coordinates so that the epipoles are at the origins, and so that corresponding epipolar lines have identical coordinates. Hence, the last row and column of F vanish, and a short calculation shows that it has the form:

$$F' = \left( \begin{array}{ccc} 0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{array}\right)$$

Let A and A' be the $3\times3$ matrices associated with this coordinate transformation in respectively the first and second image. K becomes respectively AK and A'K and the projection matrices become AP and A'P'.

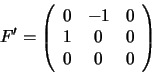
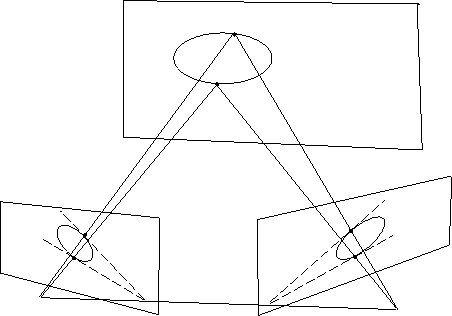
Consider a plane passing through the two camera centers and tangent to the absolute conic. This plane projects to a corresponding pair of epipolar lines in the images, which are tangent to the IAC's by construction. In fact there are two such tangential planes, so there are two pairs of corresponding epipolar tangents to the IAC's (see fig. 5.5).

  

Figure 5.5: The two epipolar tangent planes to the absolute conic define two pairs of corresponding epipolar tangents to the IAC's

Tangent lines to conics are most easily expressed in terms of dual conics ([23]). The dual conic defines the locus of lines tangent to the original conic, expressed in terms of their dual (line 3-vector) coordinates. In a coordinate frame, the dual of a conic is given by the inverse of the original conic matrix. A line (u, v, w)^t is tangent to a point conic defined by symmetric matrix C if and only if (u, v, w) C^-1 (u, v, w)^t = 0, in other words, if and only if the line vector belongs to the dual conic C^-1.

Hence, we consider the DIAC's or duals of the images of the absolute conic D=K^tA^tAK and D'=K^tA'^tA'K. After our change of coordinates, corresponding epipolar lines have identical coordinates and all pass through the origin. Let $l=(\lambda, \mu, 0)^{t}$ be an epipolar tangent to the IAC. Then in each image we have a tangency constraint: l^t D l =0 and l^t D' l=0. Expanding and using the symmetry of D and D' gives

$$\begin{eqnarray*}\lambda^{2}d_{11} + 2\lambda\mu d_{12} + \mu^{2} d_{22} &=& 0 \\ \lambda^{2}d'_{11} + 2\lambda\mu d'_{12} + \mu^{2} d'_{22} &=& 0 \end{eqnarray*}$$

Since the tangents are corresponding epipolar lines, these two quadratics must have the same solutions for $(\lambda, \mu)$. Hence, they must be identical up to a scale factor:

$$\frac{d_{11}}{d'_{11}} = \frac{d_{12}}{d'_{12}} = \frac{d_{22}}{d'_{22}}$$ (5.5)

These are the Kruppa equations.