 |
The study of projective geometry was initiated by the painters of the Italian Renaissance, who wanted to produce a convincing illusion of 3D depth in their architectural paintings. They made considerable use of vanishing points and derived several practically useful geometric constructions, for example to split a projected square into four equal sub-squares, or to find the projection of a parallelogram when the projection of two of its sides are known.
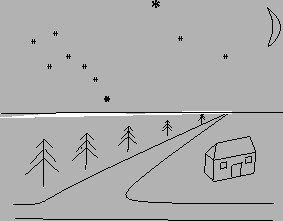
Look at figure 1.1: the edges of the road are parallel lines in 3D space, but in the image they appear to converge as they recede towards the horizon. The line of the horizon is formed by the ``infinitely distant points'' or vanishing directions of the ground plane. Any pair of parallel, horizontal lines appears to meet at the point of the horizon corresponding to their common direction. This is true even if they lie at different heights above the ground plane. Moreover, any two horizontal planes appear to come together in the distance, and intersect in the horizon line or ``line at infinity''.
All of these ``intersections at infinity'' stay constant as the observer moves. The road always seems to disappear at the same point (direction) on the horizon, and the stars stay fixed as you walk along: lines of sight to infinitely distant points are always parallel, because they ``(only) meet at infinity''.
These simple examples show that our usual concepts of finite geometry have to be extended to handle phenomena ``at infinity'' that project to very finite locations in images.