Hyperplane Transformations

In a projective space, a collineation can be defined by its 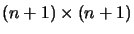$(n+1)\times(n+1)$ matrix M with respect to some fixed basis. If X and X' are the coordinate vectors of the original and transformed points, we have

X^' = MX.

This maps hyperplanes of points to transformed hyperplanes, and we would like to express this as transformation of dual (hyperplane) coordinates. Let A and A' be the original and transformed hyperplane coordinates. For all points X we have:

$$AX = 0 \Longleftrightarrow A'X' = 0 \Longleftrightarrow A'MX = 0$$

The correct transformation is therefore A'M = A or:

A' = A M^-1

or if we choose to represent hyperplanes by column vectors:

A'^t = (M^-1)^t A^t

Of course, all of this is only defined up to a scaling factor. The matrix M^* = (M^-1)^t is sometimes called the dual of M.