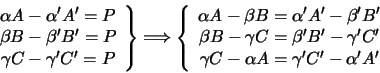 |
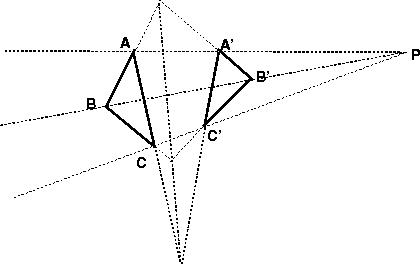
Projective geometry was invented by the French mathematician Desargues (1591-1661) (for a biography in French, see http://bib1.ulb.ac.be/coursmath/bio/desargue.htm). One of his theorems is considered to be a cornerstone of the formalism. It states that ``Two triangles are in perspective from a point if and only if they are in perspective from a line'' (see fig. 2.1):
Theorem: Let A, B, C and A', B, C' be two triangles in the (projective) plane. The lines AA', BB', CC' intersect in a single point if and only if the intersections of corresponding sides (AB, A'B'), (BC, B'C'), (CA, C'A') lie on a single line.
We will give an algebraic proof: Let P be the common intersection of
AA', BB', CC'. Hence there are scalars
![]() such that:
such that: