Projective Bases for the Projective Plane:

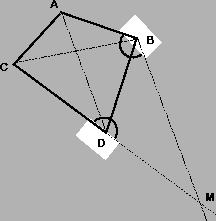
Any four distinct coplanar points (no three of which are collinear) form a projective basis for the plane they span. Given four such points A,B,C,D, a fifth point M in the plane can be characterized as the intersection of one line of the pencil through D with one line of the pencil through B (see fig. 3.2). Hence, M can be parameterized by two cross ratios (one for each pencil). This construction fails when Mlies on the line DB: in this case, another family of pencils has to be considered. This is a common phenomenon in projective spaces: a single system of coordinates does not cover the entire space without singularities or omissions.

  

Figure 3.2: Locating a fifth point in a plane

Four-point bases can be used directly for visual reconstruction of coplanar 3D points. Given four known points on a 3D plane and their perspective images, a fifth unknown point on the plane can be reconstructed from its image by expressing the image in terms of the four known image points, and then using the same homogeneous planar coordinates 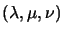$(\lambda,\mu,\nu)$ to re-create the corresponding 3D point.