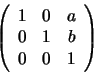Homogeneous Coordinates

How can we handle all this mathematically? -- Every point in an image represents a possible line of sight of an incoming light ray: any 3D point along the ray projects to the same image point, so only the direction of the ray is relevant, not the distance of the point along it. In vision we need to represent this ``celestial'' or ``visual sphere'' of incoming ray directions. One way to do this is by their two image (e.g. pixel) coordinates (x,y). Another is by arbitrarily choosing some 3D point along each ray to represent the ray's direction. In this case we need three ``homogeneous coordinates'' instead of two ``inhomogeneous'' ones to represent each ray. This seems inefficient, but it has the significant advantage of making the image projection process much easier to deal with.

In detail, suppose that the camera is at the origin (0,0,0). The ray represented by ``homogeneous coordinates'' (X,Y,T) is that passing through the 3D point (X,Y,T). The 3D point $\lambda\cdot(X,Y,T)=(\lambda X,\lambda Y,\lambda T)$ also lies on (represents) the same ray, so we have the rule that rescaling homogeneous coordinates makes no difference:

$$(X, Y, T) \sim \lambda(X, Y, T) = (\lambda X, \lambda Y, \lambda T)$$

If we suppose that the image plane of the camera is T=1, the ray through pixel (x,y) can be represented homogeneously by the vector $(x,y,1)\sim(xT,yT,T)$ for any depth $T\not=0$. Hence, the homogeneous point vector (X,Y,T) with $T\not=0$ corresponds to the inhomogeneous image point $(\frac{X}{T},\frac{Y}{T})$ on the plane T=1.

But what happens when T=0? -- (X,Y,0) is a valid 3D point that defines a perfectly normal optical ray, but this ray does not correspond to any finite pixel: it is parallel to the plane T=1 and so has no finite intersection with it. Such rays or homogeneous vectors can no longer be interpreted as finite points of the standard 2D plane. However, they can be viewed as additional ``ideal points'' or limits as (x,y) recedes to infinity in a certain direction:

$$\lim_{T\to 0}~(\frac{X}{T},\frac{Y}{T}, 1) \sim \lim_{T\to 0}~(X,Y,T) = (X,Y,0)$$

We can add such ideal points to any 3D plane. In 2D images of the plane, the added points at infinity form the plane's ``horizon''. We can also play the same trick on the whole 3D space, representing 3D points by four homogeneous coordinates $(X,Y,Z,T)\sim(\lambda X,\lambda Y,\lambda Z,\lambda T)\sim(\frac{X}{T},\frac{Y}{T},\frac{Z}{T},1)$ and adding a ``plane at infinity'' T=0 containing an ``ideal point at infinity'' for each 3D direction, represented by the homogeneous vector (X,Y,Z,0). This may seem unnecessarily abstract, but it turns out that 3D visual reconstruction is most naturally expressed in terms of such a ``3D projective space'', so the theory is well worth studying.

Line coordinates: The planar line with equation ax + by +c = 0is represented in homogeneous coordinates by the homogeneous equation $(a,b,c)\cdot(X,Y,T)=aX + bY + cT = 0$. If the line vector (a,b,c)is (0,0,1) we get the special ``line'' T=0 which contains only ideal points and is called the line at infinity. Note that lines are represented homogeneously as 3 component vectors, just as points are. This is the first sign of a deep and powerful projective duality between points and lines.

Now consider an algebraic curve. The standard hyperbola has equation xy = 1. Substitute $x = \frac{X}{T}, y = \frac{Y}{T}$ and multiply out to get XY = T². This is homogeneous of degree 2. In fact, in homogeneous coordinates, any polynomial can be re-expressed as a homogeneous one. Notice that $(0,\lambda,0)$ and $(\lambda,0,0)$ are valid solutions of XY = T²: the homogeneous hyperbola crosses the $\vec{x}$ axis smoothly at $y=\infty$ and the $\vec{y}$ axis smoothly at $x=\infty$, and comes back on the other side (see fig. 1.2).

  

Figure: Projectively, the hyperbola is continuous as it crosses the $\vec{x}$ and $\vec{y}$ axes

Exercise 1.1   : Consider the parabola y = x². Translate this into homogeneous coordinates and show that the line at infinity is tangent to it. Interpret the tangent geometrically by considering the parabola as the limit as k tends to $\infty$ of the ellipse 2kx² + (y-k)² - k² = 0 (hint: this has tangent y=2k).

Exercise 1.2   : Show that translation of a planar point by (a,b) is equivalent to multiplying its homogeneous coordinate column vector by

$$\left( \begin{array}{ccc} 1 & 0 & a\\ 0 & 1 & b\\ 0 & 0 & 1 \end{array}\right)$$

Exercise 1.3   :  Show that multiplying the affine (i.e. inhomogeneous) coordinates of a point by a $2\times 2$ matrix A is equivalent to multiplying its homogeneous coordinates by

$$\left( \begin{array}{c\vert c} A & \begin{array}{c} 0\\ 0 \end{array} \\ \hline 0~~0 & 1 \end{array}\right)$$

What is the homogeneous transformation matrix for a point that is rotated by angle $\theta$ about the origin, then translated by (a,b)?