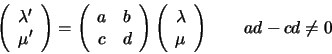Cross-Ratios on the Projective Line

Let M and N be two distinct points of a projective space. The dimension of the underlying space is irrelevant: they might be points in the projective line, plane or 3D space, hyperplanes, etc. The projective line between M and N consists of all points A of the form

$$A = \lambda M + \mu N$$

Here $(\lambda, \mu)$ are the coordinates of A in the 2D linear subspace spanned by the coordinate vectors M and N. Projectively, $(\lambda, \mu)$ are only defined up to an overall scale factor, so they really represent homogeneous coordinates on the abstract projective line $I\!\!P^1$ from M to N, expressed with respect to the linear basis of coordinate vectors $\{M,N\}$.

Let $A_i, i=1,\ldots, 4$ be any four points on this line. Their cross ratio $\{A_{1}, A_{2} ; A_{3}, A_{4}\}$ is defined to be:

 

$$\{A_1,A_2; A_3,A_4\} \frac{(\lambda_1\mu_3-\lambda_3\mu_1)(\lambda_2\mu_4-\lambda_4\mu_2)} {(\lambda_1\mu_4-\lambda_4\mu_1)(\lambda_2\mu_3-\lambda_3\mu_2)}$$ = (3.1)

$$\frac{(\lambda_1/\mu_1-\lambda_3/\mu_3)(\lambda_2/\mu_2-\lambda_4/\mu_4)} {(\lambda_1/\mu_1-\lambda_4/\mu_4)(\lambda_2/\mu_2-\lambda_3/\mu_3)}$$ =

$a/0=\infty$ is a permissable value for the cross ratio. If the numerator and denominator both vanish at least three of the $\lambda/\mu$ must be identical, so by l'Hôpital's rule the cross ratio is 1. The key property of the cross ratio is that it is invariant under collineations and changes of basis. In other words, it is a projective invariant.

Theorem: The cross ratio does not depend on the choice of basis M and N on the line. If H is a collineation, then $\{A_{1}, A_{2} ; A_{3}, A_{4}\}$ = $\{H A_{1}, H A_{2}; H A_{3}, H A_{4}\}$.

See [23] for detailed proofs. In fact, invariance under collineations need only be verified on the projective line $I\!\!P^1$:

Exercise 3.1   :  On the projective line, collineations are represented by nonsingular $2\times 2$ matrices:

$$\left( \begin{array}{c} \lambda ' \\ \mu ' \end{array} \right... ...ray}{c} \lambda \\ \mu \end{array} \right) \qquad ad-cd\not= 0$$

Show explicitly that the cross ratio is collineation invariant (Hint: $\lambda\mu'-\lambda'\mu=\hbox{det}{\lambda\;\lambda'\choose\mu\;\mu'}$).