Exercise 3.2
:
Let
D be the point at infinity on the projective line, and let
A,
B,
C be three finite points. Show that
Exercise 3.3
If
MN is the line between two points
M and
N in the projective
plane, use the
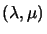
parameterization and the results of
section
2.2.1 to show that the cross ratio of four points
A,
B,
C,
D on the line is