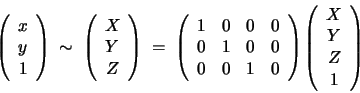


Next: Real Cameras
Up: The Perspective Camera
Previous: The Perspective Camera
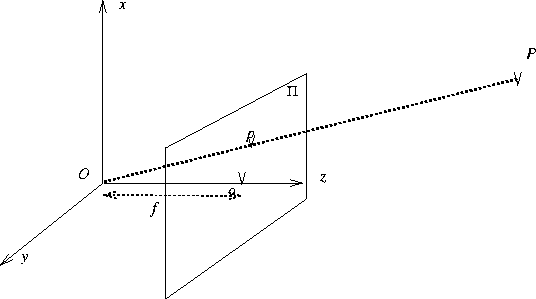
Following Dürer and the Renaissance painters, perspective
projection can be defined as follows (see fig.
1.3). The center of projection is at the
origin O of the 3D reference frame of the space. The image plane
 is parallel to the
is parallel to the
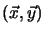 plane and displaced a
distance f (focal length) along the
plane and displaced a
distance f (focal length) along the 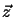 axis from the
origin. The 3D point P projects to the image point p. The
orthogonal projection of O onto
axis from the
origin. The 3D point P projects to the image point p. The
orthogonal projection of O onto 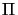 is the principal point
o, and the
is the principal point
o, and the 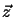 axis which corresponds to this projection line
is the principal axis (sometimes called the optical axis
by computer vision people, although there is no optic here at all).
axis which corresponds to this projection line
is the principal axis (sometimes called the optical axis
by computer vision people, although there is no optic here at all).
Figure 1.3:
Standard perspective projection
 |
Let (x, y) be the 2D coordinates of p and (X, Y, Z) the 3D
coordinates of P. A direct application of Thales theorem shows that:
We can assume that f=1 as different values of f just correspond to
different scalings of the image. Below, we will incorporate a full
camera calibration into the model. In homogeneous coordinates, the
above equations become:
In real images, the origin of the image coordinates is not the
principal point and the scaling along each image axis is different, so
the image coordinates undergo a further transformation described by
some matrix K. Also, the world coordinate system does not usually
coincide with the perspective reference frame, so the 3D coordinates
undergo a Euclidean motion described by some matrix M (see exercise
1.3), and finally we have:
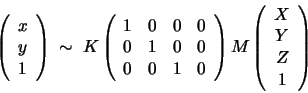 |
(1.1) |
M gives the 3D position and pose of the camera and therefore has six
degrees of freedom which represent the exterior (or extrinsic) camera parameters. In a minimal parametrization, M has
the standard 6 degrees of freedom of a rigid motion. K is
independent of the camera position. It contains the interior (or
intrinsic) parameters of the camera. It is usually represented
as an upper triangular matrix:
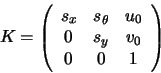 |
(1.2) |
where sx and sy stand for the scalings along the 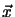 and
and 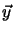 axes of the image plane,
axes of the image plane,
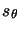 gives the skew
(non-orthogonality) between the axes (usually
gives the skew
(non-orthogonality) between the axes (usually
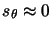 ),
and
(u0, v0) are the coordinates of the principal point
(the intersection of the principal axis and the image plane).
),
and
(u0, v0) are the coordinates of the principal point
(the intersection of the principal axis and the image plane).
Note that in homogeneous coordinates, the perspective projection model
is described by linear equations: an extremely useful property for a
mathematical model.



Next: Real Cameras
Up: The Perspective Camera
Previous: The Perspective Camera
Bill Triggs
1998-11-13
![]() is parallel to the
is parallel to the
![]() plane and displaced a
distance f (focal length) along the
plane and displaced a
distance f (focal length) along the ![]() axis from the
origin. The 3D point P projects to the image point p. The
orthogonal projection of O onto
axis from the
origin. The 3D point P projects to the image point p. The
orthogonal projection of O onto ![]() is the principal point
o, and the
is the principal point
o, and the ![]() axis which corresponds to this projection line
is the principal axis (sometimes called the optical axis
by computer vision people, although there is no optic here at all).
axis which corresponds to this projection line
is the principal axis (sometimes called the optical axis
by computer vision people, although there is no optic here at all).